Toy Problems: Prime Number Finder in 3 easy steps

Yesterday, we got a toy problem in which we need to find if a number was a prime number or not. Here’s how I went about solving the problem

1. Write some tests

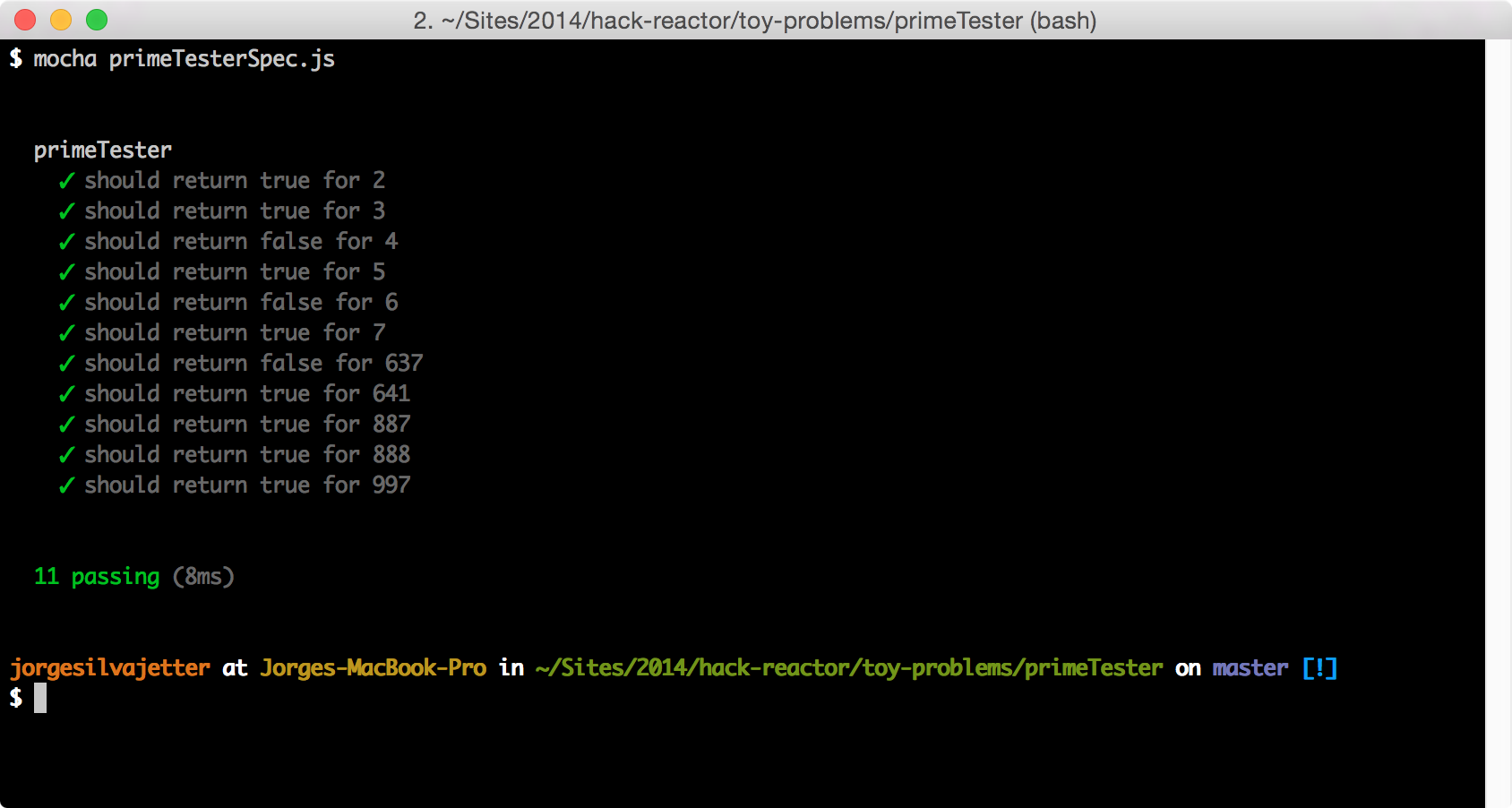
Obviously, the first thing I did was write some tests for this. I’m really, really bad at finding bugs and I’m usually too optimistic about my own solution to a problem. For me, it’s easier and more time-efficient to first write a good, complete tests suite in order to focus on coding and not think as much about testing and have a good level of confidence that my answer is correct.

Fortunately, testing this functions was pretty easy, since you just need to check for a boolean.

  it("should return true for 2", function () {
    expect(primeTester(2)).to.equal(true);
  });

  it("should return true for 3", function () {
    expect(primeTester(3)).to.equal(true);
  });

  it("should return false for 4", function () {
    expect(primeTester(4)).to.equal(false);
  });

  it("should return true for 5", function () {
    expect(primeTester(5)).to.equal(true);
  });

  it("should return false for 6", function () {
    expect(primeTester(6)).to.equal(false);
  });

  it("should return true for 7", function () {
    expect(primeTester(7)).to.equal(true);
  });

  it("should return false for 637", function () {
    expect(primeTester(637)).to.equal(false);
  });

  it("should return true for 641", function () {
    expect(primeTester(641)).to.equal(true);
  });

And that looks something like this:

2. Writing a simple, naive implementation

Now that I have some tests, it’s easy to first try to solve the problem and then optimize and refactor. For my initial implementation, I just went through all the number lower than n and then used the modulo operator to see if the number was divisible by only 1 and itself. In order to save us from some unnecessary operations, we’ll limit the number to Math.sqrt(2). The reason for using Math.sqrt(2) is that it’s impossible for a number to be divisible by a number that is higher that its square root.

var primeTester = function (n) {
  if (typeof n !== 'number' || n < 1 || n % 1 !== 0) {
     return false;
   }
  for (var i = 2; i <= Math.sqrt(n); i += 1) {
    if (n % i === 0) return false;
  }
  return true;
};

Yey! It works! How about we make this better.

3. Optimizing with primeSieve

The problem with our solution is that it goes over many numbers that we don’t have to go over. If a number is not divisible by 2, it’s certainly not divisible by 4, 8, 12, etc. In reality, we only need to check if that number is divisible by other prime numbers. In order to test whether 11 is prime, we only need to check if it’s divisible by 2, 3, 5, and 7. Actually, following our rule that we only need to test it against number that are lower than it’s square root, we only need to check it against number than are lower than 3.31 (11’s square root).

In order to get all the prime numbers, we can use the Sieve of Eratosthenes to find all prime number up to Math.sqrt(n).

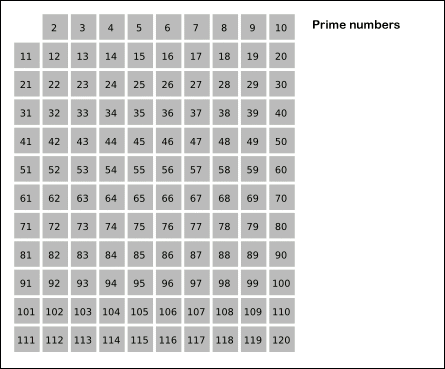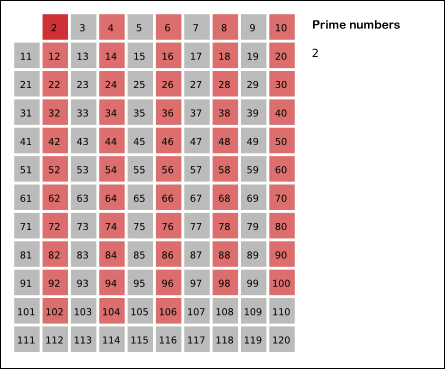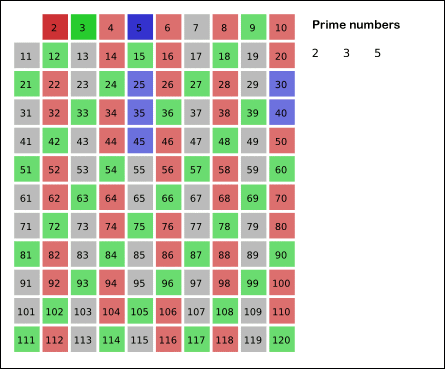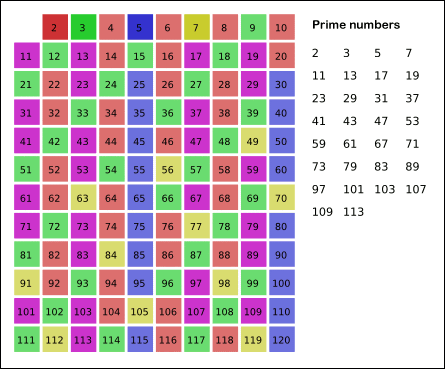
The way the siege of Eratosthenes works is that it creates an array with all the numbers up to n and goes through each one, removing all the numbers divisible by n. After it’s gone through all the array with n = 2, it increases n by 1 and loops through all the numbers again. When we do this for every number up to n, we get all the prime numbers up to n, since they’re not divisible be any number before them.

var primeSieve = function (n) {
  var numbers = range(2, n + 1);
  var loopThroughN = function (numberIndex) {
    var localN = numbers[numberIndex];
    if (n === localN || numberIndex >= numbers.length) {
      return numbers;
    }
    for (var i = 0; i < numbers.length; i += 1) {
      if (numbers[i] !== localN && numbers[i] % localN === 0) {
        numbers.splice(i, 1);
      }
    }
    return loopThroughN(numberIndex + 1);
  };
  return loopThroughN(0);
};

Using this sieve, we can now change our function so that it only divides our number by other prime numbers, minimizing the number of operations it needs to do.

var primeTester = function (n) {
  if (typeof n !== 'number' || n < 1 || n % 1 !== 0) {
    // n isn't a number or n is less than 1 or n is not an integer
    return false;
  }
  var primes = primeSieve(Math.floor(Math.sqrt(n)));
  for (var i = 0; i < primes.length; i += 1) {
    if (n !== primes[i] && n % primes[i] === 0) return false;
  }
  return true;
};

If you want to make this function even faster, you can use the sieve of Atkin to make the lookup of prime numbers even faster!

Does it pass the test?

And that’s the sweet, sweet green sound of success!